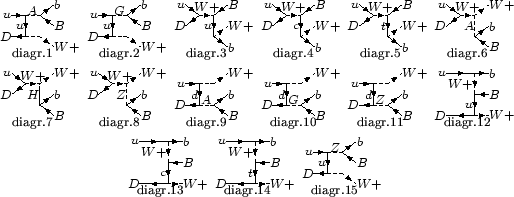Next: Основные результаты
Up: Феноменология электрослабого рождения топ-кварков
Previous: Процессы с рождением топ-кварка.
Оглавление
Как было отмечено выше, конечная сигнатура событий с рождением одиночного
топ-кварка следующая:
В такую сигнатуру дают вклад процессы, проходящие без
электрослабого рождения топ-кварка (фоновые процессы):
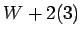 ,
,
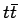 и
и
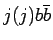 КХД события, в которых одна из струй идентифицируется как электрон.
КХД события, в которых одна из струй идентифицируется как электрон.
Полное сечение  фона, более чем на два порядка превышает сигнальное.
Этот процесс включает 32 подпроцесса для
фона, более чем на два порядка превышает сигнальное.
Этот процесс включает 32 подпроцесса для 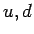 -кварков и глюонов в начальном
состоянии [15] и полное сечение составляет 1240 pb для Tevatron и 7500 pb
для LHC. Особенность процессов с рождением одиночного топ-кварка состоит в рождении
высоко энергичного
-кварков и глюонов в начальном
состоянии [15] и полное сечение составляет 1240 pb для Tevatron и 7500 pb
для LHC. Особенность процессов с рождением одиночного топ-кварка состоит в рождении
высоко энергичного  (от топ-кварка) и одного дополнительного
(от топ-кварка) и одного дополнительного  . Следовательно можно
применить дополнительное условие - идентификации
. Следовательно можно
применить дополнительное условие - идентификации  струй в событиях. В
расчетах, выполненных в данной
главе, эффективность регистрации двух
струй в событиях. В
расчетах, выполненных в данной
главе, эффективность регистрации двух  струй принята равной 50% .
Однако, даже после требования двойного
струй принята равной 50% .
Однако, даже после требования двойного  -тагирования вклад от легких
кварков остается большим. Основываясь на оценках из работы [45]
эффективность неправильной идентификации легких струй, как
-тагирования вклад от легких
кварков остается большим. Основываясь на оценках из работы [45]
эффективность неправильной идентификации легких струй, как  струй, принята равной 0.5% .
На рисунке 1.9 представлены основные диаграммы для фона
струй, принята равной 0.5% .
На рисунке 1.9 представлены основные диаграммы для фона 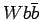 (через глюон и порядка
(через глюон и порядка
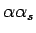 , и
, и 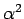 ). Так как диаграммы
для
). Так как диаграммы
для  и
и  процессов существенно отличаются (следовательно отличается
и кинематика), эти процессы рассмотрены отдельно.
процессов существенно отличаются (следовательно отличается
и кинематика), эти процессы рассмотрены отдельно.
Figure:
Диаграммы для 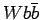 фона.
фона.
 |
Основной вклад в 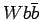 процесс дают КХД подпроцессы (диаграммы 1.9 a)
с сечением 8.7 pb для Tevatron и 30 pb для LHC
при следующих начальных обрезаниях:
процесс дают КХД подпроцессы (диаграммы 1.9 a)
с сечением 8.7 pb для Tevatron и 30 pb для LHC
при следующих начальных обрезаниях:
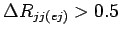 ,
, 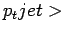 10 ГэВ для Tevatron;
10 ГэВ для Tevatron;
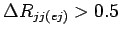 ,
, 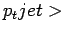 20 ГэВ для LHC.
20 ГэВ для LHC.
Диаграммы с виртуальным фотоном ( 1.9 c) составляют всего 1% от полного
сечения. Вклад от процесса  может быть подавлен обрезанием на инвариантную массу
может быть подавлен обрезанием на инвариантную массу
 . В древесном приближении сечение
. В древесном приближении сечение  составляет 2.5 pb для Tevatron и 30 pb
для LHC. Используя NLO вычисления [46], эти сечения умножаются на
k-фактор=1.33 (1.55) для
Tevatron (LHC). Процесс с рождением Хиггс бозона не существенен: его сечение на порядок
меньше чем
составляет 2.5 pb для Tevatron и 30 pb
для LHC. Используя NLO вычисления [46], эти сечения умножаются на
k-фактор=1.33 (1.55) для
Tevatron (LHC). Процесс с рождением Хиггс бозона не существенен: его сечение на порядок
меньше чем  .
.
Значительная часть фона возникает от парного рождение топ-кварков в сильных взаимодействиях,
когда один из топ-кварков распадается по адронной моде распада  , а другой по лептонной.
Основным обрезанием, дающим возможность уменьшить этот фон, является ограничение
на число струй в событии. На партонном уровне это обрезание практически подавляет
данный процесс, но после моделирования адронизации и отклика детектора необходимо
вводить дополнительные обрезания, описанные ниже. Полное NLO сечение для этого фона, полученное в
работе [48], составляет 7.5 pb на Tevatron и 760 pb на LHC.
, а другой по лептонной.
Основным обрезанием, дающим возможность уменьшить этот фон, является ограничение
на число струй в событии. На партонном уровне это обрезание практически подавляет
данный процесс, но после моделирования адронизации и отклика детектора необходимо
вводить дополнительные обрезания, описанные ниже. Полное NLO сечение для этого фона, полученное в
работе [48], составляет 7.5 pb на Tevatron и 760 pb на LHC.
Другой важный фон идет от многоструйных КХД процессов в случае, когда одна из
струй ложно идентифицируется в детекторе как электрон. Вероятность такой
ошибочной идентификации мала (примерно 0.01-0.03 %) [49], но поскольку сечение таких
процессов велико вклад в полный фон получается существенным.
Было вычислено полное сечение и созданы МК события для процессов 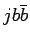 и
и 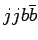 .
Вычисленные сечения по подпроцессам показаны в таблицах 1.1, 1.2.
.
Вычисленные сечения по подпроцессам показаны в таблицах 1.1, 1.2.
Table:
Сечения подпроцессов
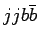 для Tevatron и LHC с обрезаниями:
для Tevatron и LHC с обрезаниями:
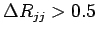 ,
, 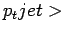 10 ГэВ для Tevatron и
10 ГэВ для Tevatron и
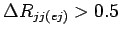 ,
,
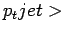 20 ГэВ для LHC.
20 ГэВ для LHC.
| process |
Tevatron (pb) |
LHC (pb) |
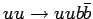 |
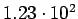 |
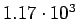 |
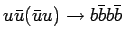 |
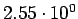 ------ ------ |
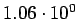 ( (
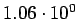 ) ) |
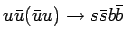 |
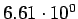 ------ ------ |
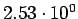 ( (
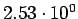 ) ) |
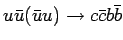 |
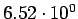 ------ ------ |
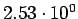 ( (
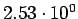 ) ) |
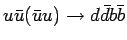 |
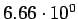 ------ ------ |
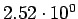 ( (
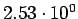 ) ) |
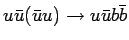 |
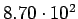 ------ ------ |
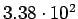 ( (
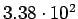 ) ) |
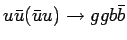 |
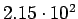 ------ ------ |
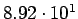 ( (
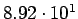 ) ) |
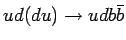 |
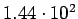 ( (
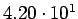 ) ) |
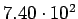 ( (
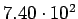 ) ) |
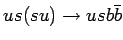 |
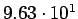 ------ ------ |
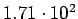 ( (
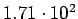 ) ) |
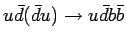 |
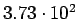 ( (
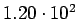 ) ) |
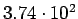 ( (
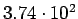 ) ) |
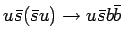 |
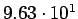 ------ ------ |
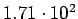 ( (
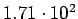 ) ) |
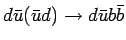 |
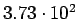 ( (
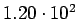 ) ) |
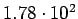 ( (
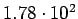 ) ) |
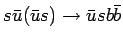 |
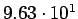 ------ ------ |
------ ------ |
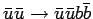 |
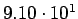 ------ ------ |
------ ------ |
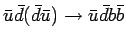 |
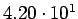 ( (
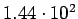 ) ) |
------ ------ |
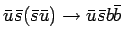 |
------ (
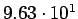 ) ) |
------ ------ |
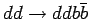 |
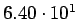 |
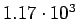 |
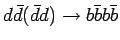 |
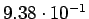 ( (
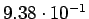 ) ) |
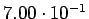 ( (
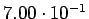 ) ) |
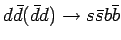 |
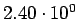 ( (
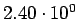 ) ) |
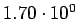 ( (
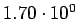 ) ) |
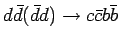 |
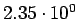 ( (
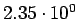 ) ) |
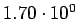 ( (
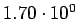 ) ) |
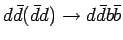 |
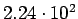 ( (
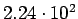 ) ) |
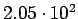 ( (
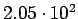 ) ) |
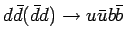 |
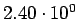 ( (
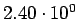 ) ) |
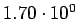 ( (
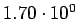 ) ) |
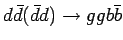 |
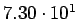 ( (
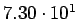 ) ) |
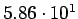 ( (
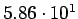 ) ) |
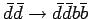 |
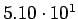 |
------ |
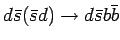 |
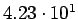 ------ ------ |
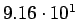 ( (
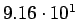 ) ) |
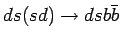 |
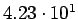 ------ ------ |
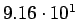 ( (
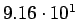 ) ) |
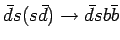 |
------
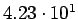 |
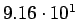 ( (
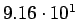 ) ) |
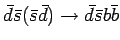 |
------
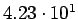 |
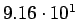 ( (
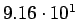 ) ) |
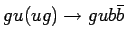 |
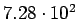 ( (
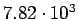 ) ) |
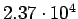 ( (
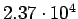 ) ) |
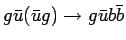 |
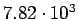 ( (
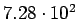 ) ) |
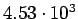 ( (
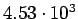 ) ) |
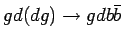 |
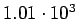 ( (
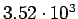 ) ) |
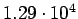 ( (
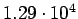 ) ) |
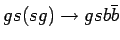 |
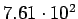 ( (
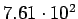 ) ) |
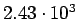 ( (
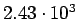 ) ) |
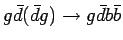 |
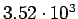 ( (
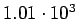 ) ) |
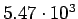 ( (
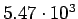 ) ) |
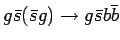 |
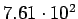 ( (
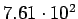 ) ) |
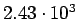 ( (
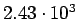 ) ) |
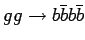 |
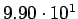 |
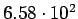 |
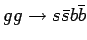 |
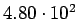 |
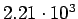 |
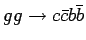 |
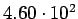 |
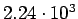 |
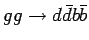 |
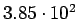 |
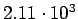 |
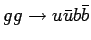 |
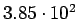 |
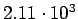 |
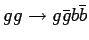 |
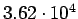 |
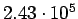 |
| Total |
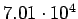 pb pb |
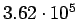 pb pb |
|
Было использовано два способа вычислений 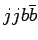 процесса. В первом проводится точное
вычисление полного набора древесных диаграмм. Во втором используется приближение функции
расщепления; при этом
вычисляется процесс
процесса. В первом проводится точное
вычисление полного набора древесных диаграмм. Во втором используется приближение функции
расщепления; при этом
вычисляется процесс 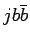 и разыгрывается дополнительная струя, идущая от излучения
из конечной или начальной линии.
и разыгрывается дополнительная струя, идущая от излучения
из конечной или начальной линии.
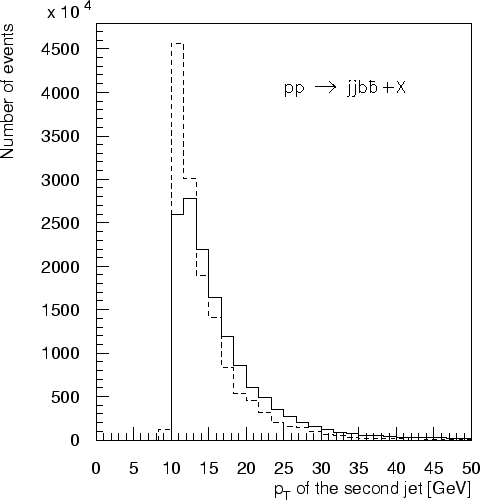
Как можно было ожидать, приближение функции расщепления дает значения полного
сечения близкие к древесным вычислениям
при условии выбора мягких обрезаний на дополнительную струю.
Но с ужесточением обрезания отличия сильно возрастают. Зависимость от обрезаний приведена
в таблице 1.3, из которой видно, что уже при обрезании
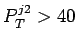 ГэВ
приближение дает примерно в 5 раз меньший результат, чем точные вычисления.
Ожидаемое различие в распределениях показанo на рисунке 1.10, из которого
видно, что получающиеся в приближении расщепления распределения существенно мягче
распределений точных древесных вычислений.
ГэВ
приближение дает примерно в 5 раз меньший результат, чем точные вычисления.
Ожидаемое различие в распределениях показанo на рисунке 1.10, из которого
видно, что получающиеся в приближении расщепления распределения существенно мягче
распределений точных древесных вычислений.
Table:
Сравнение сечений 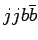 процесса при точных древесных
вычислениях и в приближении функций расщепления при различных значениях
обрезания по
процесса при точных древесных
вычислениях и в приближении функций расщепления при различных значениях
обрезания по 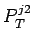 для Tevatron
с дополнительными обрезаниями на этапе генерации событий:
для Tevatron
с дополнительными обрезаниями на этапе генерации событий:
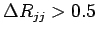 ,
,
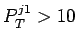 ГэВ
ГэВ
![$ p_{j2T} [ГэВ]$](img284.gif) |
10 |
15 |
20 |
40 |
![$ \sigma_{jjbb}^{exact}[nb]$](img285.gif) |
70 |
32 |
14 |
1.2 |
![$ \sigma_{jjbb}^{split}[nb]$](img286.gif) |
64 |
22 |
8 |
0.25 |
|
Figure 1.10:
Распределения по 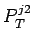 в
в 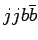 процессе, вычисленные точно на древесном уровне (сплошная линия)
и полученные в приближении функции расщепления (прерывистая линия) для Tevatron.
процессе, вычисленные точно на древесном уровне (сплошная линия)
и полученные в приближении функции расщепления (прерывистая линия) для Tevatron.
 |
Сравнивая сечения сигнальных и фоновых процессов, видно, что даже при
требовании двойного  -тагирования событий вклад фоновых процессов существенно
больше сигнальных. Следовательно, необходим подробный кинематический анализ и
выделение области фазового пространства, наиболее характерного для сигнальных событий,
что даст возможность существенно улучшить соотношение вкладов сигнальных и фоновых событий
в пользу первых.
-тагирования событий вклад фоновых процессов существенно
больше сигнальных. Следовательно, необходим подробный кинематический анализ и
выделение области фазового пространства, наиболее характерного для сигнальных событий,
что даст возможность существенно улучшить соотношение вкладов сигнальных и фоновых событий
в пользу первых.
Распределения для нескольких переменных, наиболее чувствительных к особенностям сигнальных
и фоновых событий, показаны на рисунках 1.11 для Tevatron
и на рисунках 1.12 для LHC. В эти распределения включены описанные выше
эффекты фрагментации кварков
и моделирование отклика детектора средствами пакета PYTHIA.
Для выделения сигнальных событий из фона простым кинематическим анализом были найдены следующие
наиболее привлекательные
переменные.
 наиболее энергичной струи в событии;
наиболее энергичной струи в событии;
 такой струи для сигнальных событий имеет пик примерно на значении
такой струи для сигнальных событий имеет пик примерно на значении 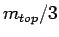 ,
в то время как в КХД и
,
в то время как в КХД и  событиях на Tevatron это значение существенно меньше,
и струи в таких событиях разлетаются под более малыми углами к направлению пучка.
При существенно большей энергии на коллайдере LHC основной вклад в фоновые
события дает парное рождение
событиях на Tevatron это значение существенно меньше,
и струи в таких событиях разлетаются под более малыми углами к направлению пучка.
При существенно большей энергии на коллайдере LHC основной вклад в фоновые
события дает парное рождение  и соотношение полных распределений для
сигнальных и фоновых событий меняется (рисунок 1.12).
и соотношение полных распределений для
сигнальных и фоновых событий меняется (рисунок 1.12).-
 - инвариантная масса рожденных частиц.
- инвариантная масса рожденных частиц.
Пик распределений для этой переменной всегда ниже для  и КХД фонов по сравнению с
сигнальными событиями. Пик в распределении для
и КХД фонов по сравнению с
сигнальными событиями. Пик в распределении для 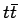 процесса
примерно в два раза выше по сравнению с сигналом.
процесса
примерно в два раза выше по сравнению с сигналом.
 :
:  -бозон, как правило, жестче от распада
-бозон, как правило, жестче от распада  кварка, чем в
кварка, чем в  процессах.
процессах.- Полная поперечная энергия
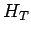 ,
,
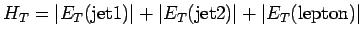 ;
для этой переменной имеется пик в районе 150 ГэВ для сигнала, 300 ГэВ для
;
для этой переменной имеется пик в районе 150 ГэВ для сигнала, 300 ГэВ для 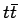 процесса
и близкий к нулю пик для КХД фонов.
процесса
и близкий к нулю пик для КХД фонов.
- Инвариантная масса двух струй.
Эта переменная жестче для сигнала, чем для КХД фонов, в которых  пара происходит,
в основном, от расщепления глюона. Распределение для
пара происходит,
в основном, от расщепления глюона. Распределение для 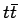 фона похоже на сигнальное.
Обрезание по этой переменной помогает подавить
фона похоже на сигнальное.
Обрезание по этой переменной помогает подавить  фон.
фон.
Figure 1.11:
Распределения сигнальных и фоновых событий по некоторым
наиболее интересным переменным для Tevatron. Заштрихованная гистограмма показывает
сигнальные события.
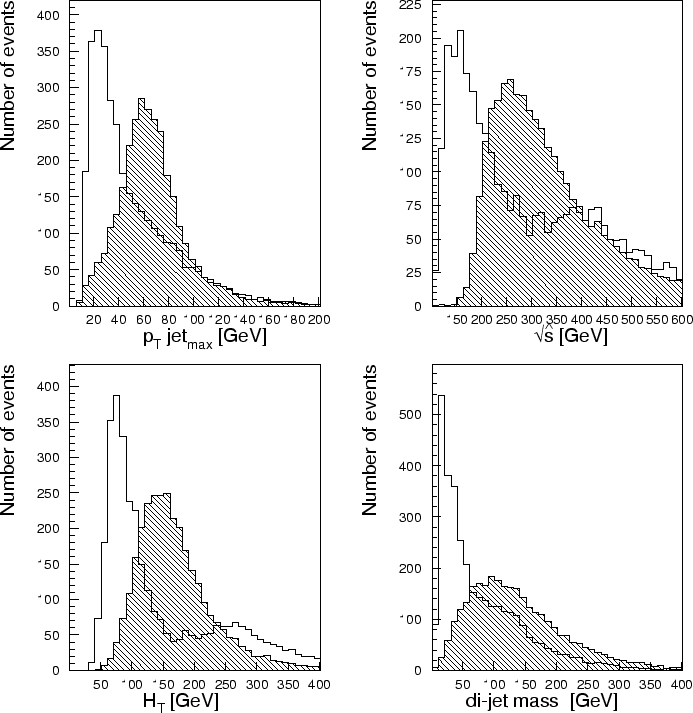 |
Figure 1.12:
Распределения сигнальных и фоновых событий по некоторым
наиболее интересным переменным для LHC. Заштрихованная гистограмма показывает
сигнальные события.
 |
Основываясь на описанных различиях в поведении распределений для сигнальных и фоновых
процессов, был выбран следующий набор обрезаний, позволяющий существенно улучшить соотношение
между сигнальными и фоновыми событиями.
| |
|
 |
(1.13) |
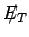 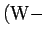  |
|
|
(1.14) |
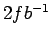 |
|
|
(1.15) |
 |
|
|
(1.16) |
 |
|
|
(1.17) |
 |
|
|
(1.18) |
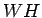 |
|
|
(1.19) |
 |
|
|
(1.20) |
 |
|
|
(1.21) |
 |
|
|
(1.22) |
Эффект последовательного применения таких обрезаний приведен в
таблицах 1.4,1.5. Приведенные числа событий в таблицах,
как и на рисунках 1.11,1.12, получены при интегральной
светимости коллайдеров 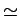 (
(
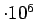 ) для Tevatron (LHC) с эффективностью
двойного
) для Tevatron (LHC) с эффективностью
двойного  тагирования 50% и вероятностью ложной идентификации
тагирования 50% и вероятностью ложной идентификации
 -кварка 0.5%.
-кварка 0.5%.
Table 1.4:
Числа событий рождения одиночного топ-кварка и фоновых событий
для Tevatron в зависимости от последовательного применения обрезаний, описанных в
тексте.
| cuts |
signal |
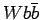 |
 |
 |
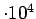 |
 |
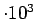 |
| Cut 1 |
1.986
 |
3.680
 |
2.644
 |
2.059
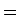 |
6.292
 |
5.849
 |
8.428
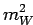 |
| Cut 2 |
1.514
 |
1.711
 |
1.034
 |
1.136
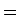 |
1.114
 |
4.898
 |
6.491
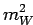 |
| Cut 3 |
1.493
 |
1.453
 |
9.211
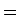 |
1.053
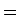 |
1.030
 |
4.898
 |
6.278
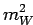 |
| Cut 4 |
1.295
 |
1.173
 |
7.687
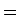 |
8.564
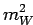 |
8.910
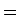 |
4.191
 |
5.145
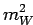 |
| Cut 5 |
1.286
 |
1.107
 |
7.488
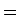 |
8.515
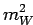 |
8.353
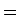 |
4.186
 |
5.124
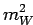 |
| Cut 6 |
1.249
 |
1.038
 |
6.649
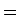 |
8.087
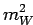 |
6.961
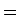 |
4.185
 |
5.013
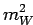 |
| Cut 7 |
1.247
 |
1.031
 |
6.649
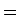 |
7.419
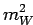 |
4.455
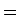 |
1.055
 |
4.562
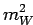 |
| Cut 8 |
1.216
 |
8.867
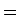 |
6.141
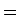 |
7.266
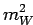 |
3.619
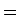 |
1.039
 |
4.490
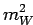 |
Signal: 122, Background: 297; S/B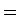 0.41 0.41 |
|
Table 1.5:
Числа событий рождения одиночного топ-кварка и
фоновых событий
для LHC в зависимости от последовательного применения обрезаний, описанных в
тексте.
| cuts |
signal |
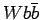 |
 |
 |
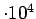 |
 |
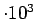 |
| Cut 1 |
1.212
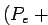 |
8.236
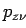 |
1.724
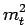 |
1.912
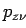 |
1.155
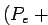 |
4.449
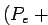 |
6.124
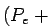 |
| Cut 2 |
8.792
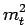 |
5.143
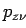 |
1.058
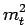 |
1.177
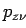 |
6.112
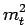 |
3.762
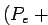 |
4.923
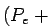 |
| Cut 3 |
8.764
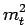 |
4.871
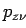 |
1.015
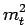 |
1.138
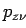 |
6.053
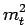 |
3.762
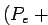 |
4.854
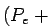 |
| Cut 4 |
7.423
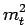 |
3.826
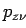 |
7.758
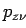 |
9.048
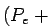 |
4.974
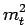 |
3.262
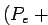 |
3.976
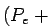 |
| Cut 5 |
7.401
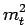 |
3.771
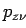 |
7.735
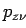 |
9.013
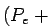 |
4.957
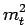 |
3.262
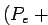 |
3.972
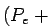 |
| Cut 6 |
5.643
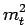 |
3.649
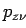 |
7.524
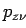 |
7.545
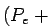 |
4.729
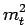 |
6.214
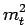 |
3.334
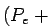 |
| Cut 7 |
5.370
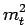 |
3.610
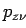 |
7.408
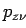 |
6.122
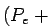 |
2.411
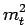 |
1.886
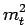 |
2.740
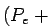 |
| Cut 8 |
5.296
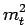 |
3.177
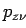 |
7.019
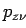 |
6.030
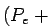 |
2.301
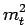 |
1.886
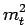 |
2.694
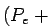 |
Signal:
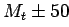 , Background: , Background:
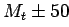 ; S/B ; S/B 1.0 1.0 |
|
В приведенном анализе используется переменная - ``эффективная'' масса топ-кварка,
вычисляемая по следующему алгоритму. При распаде топ-кварка на лептон, нейтрино
и  кварк невозможно точно реконструировать z-компоненту импульса нейтрино.
Предполагается, что регистрируемые в событии лептон и незарегистрированная
поперечная энергия происходят от распада
кварк невозможно точно реконструировать z-компоненту импульса нейтрино.
Предполагается, что регистрируемые в событии лептон и незарегистрированная
поперечная энергия происходят от распада  , следовательно должно выполняться
соотношение:
, следовательно должно выполняться
соотношение:
Решая квадратное уравнение для z-компоненты импульса нейтрино нужно выбрать один из двух
получающихся корней. Монте-Карло анализ показывает, что если выбрать
наименьший корень, то примерно в 70% случаев это будет правильный выбор.
Основная причина такой ситуации в том, что выбор наименьшего 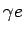 соответствует в большинстве случаев наименьшему значению
соответствует в большинстве случаев наименьшему значению  и следовательно большему сечению.
Далее ``эффективная'' масса топ-кварка определяется по следующей формуле:
и следовательно большему сечению.
Далее ``эффективная'' масса топ-кварка определяется по следующей формуле:
Фиксированный выбор решения для 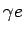 размывает пик в распределении по этой переменной;
в качестве обрезания по такой переменной было выбрано окно
размывает пик в распределении по этой переменной;
в качестве обрезания по такой переменной было выбрано окно 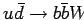 ГэВ.
ГэВ.
Подавление фона с помощью описанных обрезаний продемонстрировано на
рисунках 1.13ab, 1.14ab, где показаны распределения
по ``эффективной'' инвариантной массе топа до обрезаний (a) и после (b).
После применения обрезаний фон стал примерно в 10 (18) раз меньше на Tevatron (LHC),
в то время как, 60% (40%) сигнальных событий проходят приведенные обрезания.
Соотношение сигнальных событий к фоновым становиться примерно 0.6 на Tevatron и 1
на LHC, что позволяет измерить сечения сигнальных процессов с относительно
высокой точностью. Сечение сигнальных процессов напрямую включает 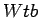 вершину,
что дает уникальную возможность прямого
изучения структуры
вершину,
что дает уникальную возможность прямого
изучения структуры 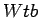 вершины и измерения
вершины и измерения 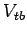 параметра с точностью
примерно 10% на Tevatron (Run II) и нескольких процентов на LHC [50].
Как будет продемонстрировано в следующей главе, результаты измерений на LHC
будут сильно зависеть от систематической ошибки, один из основных вкладов в которую,
вносит неопределенность в теоретических вычислениях сечения сигнальных процессов.
Следовательно, черезвычайно важно продолжить вычисления в следующих порядках
теории возмущений.
параметра с точностью
примерно 10% на Tevatron (Run II) и нескольких процентов на LHC [50].
Как будет продемонстрировано в следующей главе, результаты измерений на LHC
будут сильно зависеть от систематической ошибки, один из основных вкладов в которую,
вносит неопределенность в теоретических вычислениях сечения сигнальных процессов.
Следовательно, черезвычайно важно продолжить вычисления в следующих порядках
теории возмущений.
Figure 1.13:
Распределение по ``эффективной'' инвариантной
массе топ-кварка до (а) и после (b) применения обрезаний для Tevatron.
Заштрихованные гистограммы показывают сигнальные события.
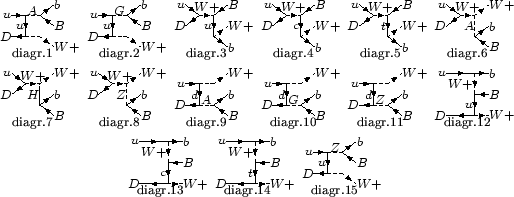 |
Figure 1.14:
Распределение по ``эффективной'' инвариантной
массе топ-кварка до (а) и после (b) применения обрезаний для Tevatron.
Заштрихованные гистограммы показывают сигнальные события.
 |




Next: Основные результаты
Up: Феноменология электрослабого рождения топ-кварков
Previous: Процессы с рождением топ-кварка.
Оглавление
![]() фона, более чем на два порядка превышает сигнальное.
Этот процесс включает 32 подпроцесса для
фона, более чем на два порядка превышает сигнальное.
Этот процесс включает 32 подпроцесса для ![]() -кварков и глюонов в начальном
состоянии [15] и полное сечение составляет 1240 pb для Tevatron и 7500 pb
для LHC. Особенность процессов с рождением одиночного топ-кварка состоит в рождении
высоко энергичного
-кварков и глюонов в начальном
состоянии [15] и полное сечение составляет 1240 pb для Tevatron и 7500 pb
для LHC. Особенность процессов с рождением одиночного топ-кварка состоит в рождении
высоко энергичного ![]() (от топ-кварка) и одного дополнительного
(от топ-кварка) и одного дополнительного ![]() . Следовательно можно
применить дополнительное условие - идентификации
. Следовательно можно
применить дополнительное условие - идентификации ![]() струй в событиях. В
расчетах, выполненных в данной
главе, эффективность регистрации двух
струй в событиях. В
расчетах, выполненных в данной
главе, эффективность регистрации двух ![]() струй принята равной 50% .
Однако, даже после требования двойного
струй принята равной 50% .
Однако, даже после требования двойного ![]() -тагирования вклад от легких
кварков остается большим. Основываясь на оценках из работы [45]
эффективность неправильной идентификации легких струй, как
-тагирования вклад от легких
кварков остается большим. Основываясь на оценках из работы [45]
эффективность неправильной идентификации легких струй, как ![]() струй, принята равной 0.5% .
На рисунке 1.9 представлены основные диаграммы для фона
струй, принята равной 0.5% .
На рисунке 1.9 представлены основные диаграммы для фона ![]() (через глюон и порядка
(через глюон и порядка
![]() , и
, и ![]() ). Так как диаграммы
для
). Так как диаграммы
для ![]() и
и ![]() процессов существенно отличаются (следовательно отличается
и кинематика), эти процессы рассмотрены отдельно.
процессов существенно отличаются (следовательно отличается
и кинематика), эти процессы рассмотрены отдельно.
![]() , а другой по лептонной.
Основным обрезанием, дающим возможность уменьшить этот фон, является ограничение
на число струй в событии. На партонном уровне это обрезание практически подавляет
данный процесс, но после моделирования адронизации и отклика детектора необходимо
вводить дополнительные обрезания, описанные ниже. Полное NLO сечение для этого фона, полученное в
работе [48], составляет 7.5 pb на Tevatron и 760 pb на LHC.
, а другой по лептонной.
Основным обрезанием, дающим возможность уменьшить этот фон, является ограничение
на число струй в событии. На партонном уровне это обрезание практически подавляет
данный процесс, но после моделирования адронизации и отклика детектора необходимо
вводить дополнительные обрезания, описанные ниже. Полное NLO сечение для этого фона, полученное в
работе [48], составляет 7.5 pb на Tevatron и 760 pb на LHC.
![]() и
и ![]() .
Вычисленные сечения по подпроцессам показаны в таблицах 1.1, 1.2.
.
Вычисленные сечения по подпроцессам показаны в таблицах 1.1, 1.2.
![]() процесса. В первом проводится точное
вычисление полного набора древесных диаграмм. Во втором используется приближение функции
расщепления; при этом
вычисляется процесс
процесса. В первом проводится точное
вычисление полного набора древесных диаграмм. Во втором используется приближение функции
расщепления; при этом
вычисляется процесс ![]() и разыгрывается дополнительная струя, идущая от излучения
из конечной или начальной линии.
и разыгрывается дополнительная струя, идущая от излучения
из конечной или начальной линии.
![]() ГэВ
приближение дает примерно в 5 раз меньший результат, чем точные вычисления.
Ожидаемое различие в распределениях показанo на рисунке 1.10, из которого
видно, что получающиеся в приближении расщепления распределения существенно мягче
распределений точных древесных вычислений.
ГэВ
приближение дает примерно в 5 раз меньший результат, чем точные вычисления.
Ожидаемое различие в распределениях показанo на рисунке 1.10, из которого
видно, что получающиеся в приближении расщепления распределения существенно мягче
распределений точных древесных вычислений.

![]() -тагирования событий вклад фоновых процессов существенно
больше сигнальных. Следовательно, необходим подробный кинематический анализ и
выделение области фазового пространства, наиболее характерного для сигнальных событий,
что даст возможность существенно улучшить соотношение вкладов сигнальных и фоновых событий
в пользу первых.
-тагирования событий вклад фоновых процессов существенно
больше сигнальных. Следовательно, необходим подробный кинематический анализ и
выделение области фазового пространства, наиболее характерного для сигнальных событий,
что даст возможность существенно улучшить соотношение вкладов сигнальных и фоновых событий
в пользу первых.


![]() кварк невозможно точно реконструировать z-компоненту импульса нейтрино.
Предполагается, что регистрируемые в событии лептон и незарегистрированная
поперечная энергия происходят от распада
кварк невозможно точно реконструировать z-компоненту импульса нейтрино.
Предполагается, что регистрируемые в событии лептон и незарегистрированная
поперечная энергия происходят от распада ![]() , следовательно должно выполняться
соотношение:
, следовательно должно выполняться
соотношение:
![]() вершину,
что дает уникальную возможность прямого
изучения структуры
вершину,
что дает уникальную возможность прямого
изучения структуры ![]() вершины и измерения
вершины и измерения ![]() параметра с точностью
примерно 10% на Tevatron (Run II) и нескольких процентов на LHC [50].
Как будет продемонстрировано в следующей главе, результаты измерений на LHC
будут сильно зависеть от систематической ошибки, один из основных вкладов в которую,
вносит неопределенность в теоретических вычислениях сечения сигнальных процессов.
Следовательно, черезвычайно важно продолжить вычисления в следующих порядках
теории возмущений.
параметра с точностью
примерно 10% на Tevatron (Run II) и нескольких процентов на LHC [50].
Как будет продемонстрировано в следующей главе, результаты измерений на LHC
будут сильно зависеть от систематической ошибки, один из основных вкладов в которую,
вносит неопределенность в теоретических вычислениях сечения сигнальных процессов.
Следовательно, черезвычайно важно продолжить вычисления в следующих порядках
теории возмущений.