В Стандартной Модели одиночный t-кварк с почти 100%
вероятностью рождается через ![]() вершину.
На адронных коллайдерах возможны три основных процесса
рождения топ-кварка; основные фейнмановские диаграммы
показаны на рисунках 1.1 и 1.2.
Наборы диаграмм не отличаются для
вершину.
На адронных коллайдерах возможны три основных процесса
рождения топ-кварка; основные фейнмановские диаграммы
показаны на рисунках 1.1 и 1.2.
Наборы диаграмм не отличаются для ![]() (Tevatron) и
(Tevatron) и ![]() (LHC)
взаимодействий; отличия проявляются на уровне партонных структурных функций и
разницы в энергии столкновений.
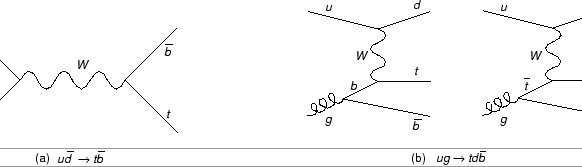
На рисунке (1.1 a) показана диаграмма для наиболее простого s-канального
процесса. На рисунке (1.1 b) показаны основные диаграммы для t-канального
процесса - в литературе часто упоминается как
(LHC)
взаимодействий; отличия проявляются на уровне партонных структурных функций и
разницы в энергии столкновений.
На рисунке (1.1 a) показана диаграмма для наиболее простого s-канального
процесса. На рисунке (1.1 b) показаны основные диаграммы для t-канального
процесса - в литературе часто упоминается как ![]() -слияние; вторая диаграмма для этого
процесса дает небольшой вклад в полное сечение - примерно 5% на Tevatron,
но отрицательная интерференция между первой и второй диаграммами составляет 30%.
Aссоциативноe
-слияние; вторая диаграмма для этого
процесса дает небольшой вклад в полное сечение - примерно 5% на Tevatron,
но отрицательная интерференция между первой и второй диаграммами составляет 30%.
Aссоциативноe ![]() рождениe имеет существенно
отличную от предыдущих процессов конечную сигнатуру, похожую на сигнатуру
парного
рождениe имеет существенно
отличную от предыдущих процессов конечную сигнатуру, похожую на сигнатуру
парного ![]() рождения. Сечение этого процесса
составляет всего несколько процентов от полного сечения на
коллайдере Tevatron
и он требует отдельного рассмотрения для LHC коллайдера. Основные
фейнмановские диаграммы для последнего процесса
приведены на рисунке 1.2, все оценки для него берутся
из статьи [32].
рождения. Сечение этого процесса
составляет всего несколько процентов от полного сечения на
коллайдере Tevatron
и он требует отдельного рассмотрения для LHC коллайдера. Основные
фейнмановские диаграммы для последнего процесса
приведены на рисунке 1.2, все оценки для него берутся
из статьи [32].
 |
При вычислении полного набора диаграмм, дающих вклад в t-канальный
процесс, возникает проблема двойного учета члена
с функцией расщепления глюона, компоненты которой содержатся,
как и в структурных функциях, так и в диаграмме
![]() (рисунок (1.3 a).
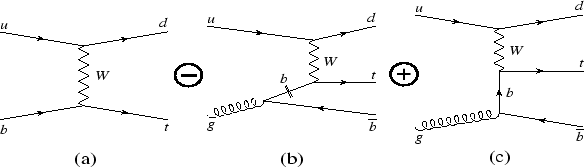
С целью корректного учета всех диаграмм была реализована схема
вычислений, схематично показанная на
рисунке (1.3); из процесса (1.3 a) на уровне структурных
функций вычитается первый член функции расщепления глюона (1.3 b) и добавляется
точно вычисленная на древесном
уровне диаграмма с глюоном в начальном состоянии (1.3 c).
(рисунок (1.3 a).
С целью корректного учета всех диаграмм была реализована схема
вычислений, схематично показанная на
рисунке (1.3); из процесса (1.3 a) на уровне структурных
функций вычитается первый член функции расщепления глюона (1.3 b) и добавляется
точно вычисленная на древесном
уровне диаграмма с глюоном в начальном состоянии (1.3 c).
 |
Такая схема была реализована при создании первой версии Монте-Карло (МК) генератора SingleTop
для моделирования t-канального процесса для Tevatron (Run I).
В более поздних вычислениях и в вычислениях для коллайдера LHC (вторая версия генератора SingleTop)
было реализовано разделение
вкладов от разных диаграмм с помощью разделяющего обрезания
на ![]() , идущего от расщепления глюона.
, идущего от расщепления глюона.
Для моделирования событий с рождением t-кварка на коллайдере
Teavatron был создан
Монте-Карло генератор (SingleTop I), содержащий полный набор
сигнальных диаграмм на древесном уровне. Генератор использует
созданные пакетом CompHEP3.0 [33] коды квадратов матричных элементов
и он продолжен интерфейсом в
пакет PYTHIA5.7/JETSET7.4 [34] методом
внешнего пользовательского процесса. Для интегрирования
по фазовому пространству, введению регуляризаций и генерации
событий использовался CompHEP и пакет интегрирования
BASES/SPRING [36]. Эффекты адронизации, излучения
из начальных и конечных линий и моделирование адронных остатков были созданы пакетом JETSET7.4.
Использовалась струнная модель фрагментации кварков.
Вычисления проводились со структурными функциями CTEQ3m
при масштабе КХД ![]() для s-канального процесса и
для s-канального процесса и
![]() для
t-канального процесса. Такой выбор
для
t-канального процесса. Такой выбор ![]() обусловлен сопоставлением
сечения в лидирующем порядке (LO) и вычисленными в
работах [37], [38]
сечениях в следующем порядке теории возмущений (NLO). Конечные результаты
вычислялись с использованием перенормирования полученного LO сечения
на NLO сечение, которое было получено для s-канального
процесса в работе [37] и t-канального процесса
в работе [38]. Результаты этих вычислений
при
обусловлен сопоставлением
сечения в лидирующем порядке (LO) и вычисленными в
работах [37], [38]
сечениях в следующем порядке теории возмущений (NLO). Конечные результаты
вычислялись с использованием перенормирования полученного LO сечения
на NLO сечение, которое было получено для s-канального
процесса в работе [37] и t-канального процесса
в работе [38]. Результаты этих вычислений
при
![]() дают:
дают:
В настоящее время развиваются несколько МК генераторов для моделирования процессов с рождением одиночного топ-кварка, такие как [39,40] ONETOP, TopRex, генераторы основанные на пакетах MADGRAPH, PYTHIA и CompHEP (первая версия последнего, описана выше). К сожалению ни один из перечисленных генераторов не решает все возникающие проблемы, к которым относятся следующие:
Как следующий шаг к решению перечисленных выше проблем, была предложена
новая схема моделирования электрослабого рождения топ-кварка (генератор - SingleTop II) в применении
к коллайдеру LHC и Tevatron (Run II). Cпособ вычисления вполне общий и он
применим и к другим процессам.
Как и в первой версии генератора, созданного для коллайдера TEVATRON, все
матричные элементы для полного набора древесных фейнмановских диаграмм
были вычислены пакетом CompHEP. Все распады были включены в матричные элементы
и таким образом была правильно смоделирована спиновая структура
для конечных состояний.
Созданные на партонном уровне события передавались через стандартный
интерфейс [41] в пакет PYTHIA6.1
для дальнейшего
моделирования адронизации кварков, излучения из конечных и начальных линий и
моделирования адронных остатков.
В таблицах 1.7, 1.8, 1.9, 1.10
приведены подпроцессы, включенные в каждый процесс. Суммирование проводилось
на уровне структурных функций, объединялись подпроцессы, имеющие одинаковую структуру
матричного элемента и отличающиеся начальными или конечными состояниями.
С целью корректной фрагментации конечных кварков их ароматы были сохранены,
поскольку имеется существенное отличие в адронизации, например ![]() и
и ![]() кварков;
кварков; ![]() и
и ![]() кварки, были объединены в один подпроцесс в связи с малыми
различиями в моделировании адронизации. В таблицах приведены парциальные и полные
сечения для достаточно жесткой кинематической области с начальными обрезаниями:
кварки, были объединены в один подпроцесс в связи с малыми
различиями в моделировании адронизации. В таблицах приведены парциальные и полные
сечения для достаточно жесткой кинематической области с начальными обрезаниями:
![]() 10 ГэВ,
10 ГэВ,
![]() 20 ГэВ (
20 ГэВ (![]() процесс), и дистанцией в
процесс), и дистанцией в
![]() параметрическом пространстве
параметрическом пространстве
![]() .
В дальнейшем будет объяснен выбор таких обрезаний.
.
В дальнейшем будет объяснен выбор таких обрезаний.
Необходимо отметить, что при энергии коллайдера LHC большой вклад дают процессы с морскими кварками в начальном состоянии. Например, для процесса 1.7 они составляют около 20% от суммарного сечения.
|
|
 |
 |
Однако пока не была рассмотрена кинематическая область с мягким ![]() кварком в конечном состоянии
для процесса
кварком в конечном состоянии
для процесса ![]() (диаграммы 1.1b), которая может быть
интересна в некоторых
исследованиях. Вычисления описанные выше, базируются на точных вычислениях
полного набора древесных
диаграмм для реакций с рождением
(диаграммы 1.1b), которая может быть
интересна в некоторых
исследованиях. Вычисления описанные выше, базируются на точных вычислениях
полного набора древесных
диаграмм для реакций с рождением ![]() кварка в ассоциации с
кварка в ассоциации с ![]() и легким кварком.
и легким кварком.
Существyют другие пути для моделирования такого же конечного состояния.
Один из наиболее
известных способов (например, использованный в работе [42]), использовать
пакет PYTHIA для части ![]() t-канального процесса с
t-канального процесса с ![]() кварком в начальном состоянии
при одновременном моделировании излучений из начальных и конечных линий, и выбирать
события с дополнительным
кварком в начальном состоянии
при одновременном моделировании излучений из начальных и конечных линий, и выбирать
события с дополнительным ![]() кварком в конечном состоянии, происходящим от расщепления
глюона, излученного из начальной или конечной линии.
Строго говоря, как первый, так и второй способ вычислений не полностью корректны во всей
области фазового
пространства. Полные
кварком в конечном состоянии, происходящим от расщепления
глюона, излученного из начальной или конечной линии.
Строго говоря, как первый, так и второй способ вычислений не полностью корректны во всей
области фазового
пространства. Полные ![]() древесные вычисления
не включают важную часть КХД коррекций, входящих в вершину расщепления глюона
в
древесные вычисления
не включают важную часть КХД коррекций, входящих в вершину расщепления глюона
в ![]() пару
и дающих основной вклад в кинематическую область с мягким конечным
пару
и дающих основной вклад в кинематическую область с мягким конечным ![]() .
Во втором способе с
.
Во втором способе с ![]() кварком в начальном состоянии учитывается большая
часть поправок, но
такой способ работает, только в кинематической области с мягким
кварком в начальном состоянии учитывается большая
часть поправок, но
такой способ работает, только в кинематической области с мягким
![]() -кварком в конечном состоянии.
Ниже описывается способ объединения этих двух методов,
при котором, будет
более правильно моделироваться и мягкая и жесткая кинематические области.
-кварком в конечном состоянии.
Ниже описывается способ объединения этих двух методов,
при котором, будет
более правильно моделироваться и мягкая и жесткая кинематические области.
Разделить мягкую и жесткую кинематическую области для конечного ![]() кварка
можно сравнив полные сечения и распределения, смоделированные описанным выше
генератором SingleTop и пакетом PYTHIA с приближением, использующим функции расщепления глюона
для моделирования конечного
кварка
можно сравнив полные сечения и распределения, смоделированные описанным выше
генератором SingleTop и пакетом PYTHIA с приближением, использующим функции расщепления глюона
для моделирования конечного ![]() . В последнем случае используется PYTHIA для процесса
. В последнем случае используется PYTHIA для процесса
![]() (ключ MSUB = 83) с одновременным моделированием
излучения из начальной и конечной линий. Далее выбираются события с топ-кварком,
легким кварком и дополнительным
(ключ MSUB = 83) с одновременным моделированием
излучения из начальной и конечной линий. Далее выбираются события с топ-кварком,
легким кварком и дополнительным ![]() кварком, идущим от расщепления начального
(или излученного) глюона.
кварком, идущим от расщепления начального
(или излученного) глюона.
Все модельные параметры, структурные функции и КХД масштаб были выбраны одинаковыми в обоих способах моделирования. Сравнение проводилось на партонном уровне для конечных частиц. Полное сечение, вычисленное без каких то начальных обрезаний, равно 235 pb в PYTHIA и 224 pb в генераторе SingleTop. Согласование сечений на уровне 5%.
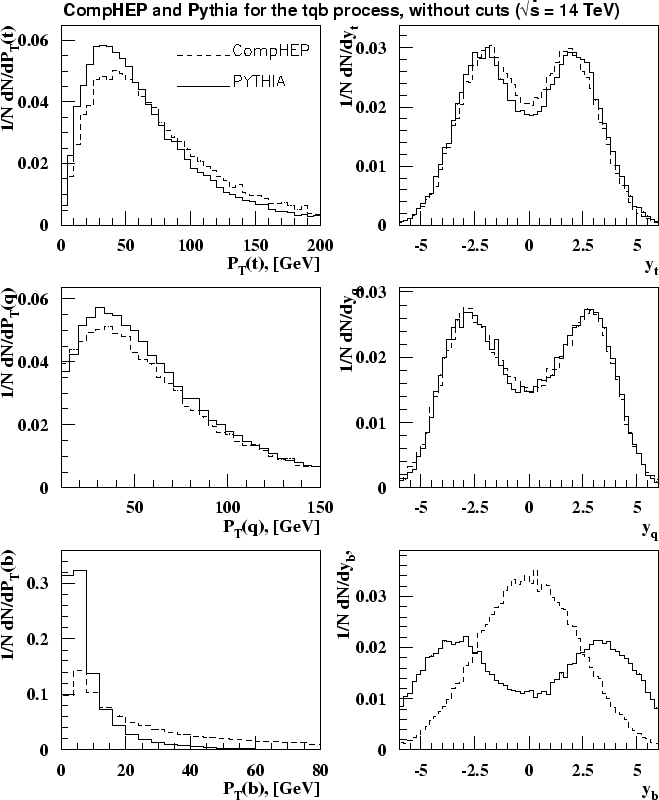
На рисунке 1.4 приводятся
распределения по ![]() и
и ![]() конечных частиц, смоделированных генератором SingleTop и
пакетом PYTHIA. Видно, что распределения для
конечных частиц, смоделированных генератором SingleTop и
пакетом PYTHIA. Видно, что распределения для ![]() и легкого кварков
совпадают; в распределениях для дополнительного
и легкого кварков
совпадают; в распределениях для дополнительного ![]() кварка имеются существенные отличия.
Как можно было ожидать,
кварка имеются существенные отличия.
Как можно было ожидать, ![]() , спектр полученный в приближении функции расщепления глюона
в PYTHIA, существенно мягче и при этом дополнительные
, спектр полученный в приближении функции расщепления глюона
в PYTHIA, существенно мягче и при этом дополнительные ![]() разлетаются под более малыми углами,
в отличии
от точных вычислений древесного матричного элемента, где
разлетаются под более малыми углами,
в отличии
от точных вычислений древесного матричного элемента, где ![]() кварк оказывается
центральным.
кварк оказывается
центральным.
Возникает вопрос, какое распределение более корректное? Ответ - каждое
не совсем корректно во всей области фазового пространства. Точные вычисления
на древесном уровне описывают жесткую кинематическую область. При применении
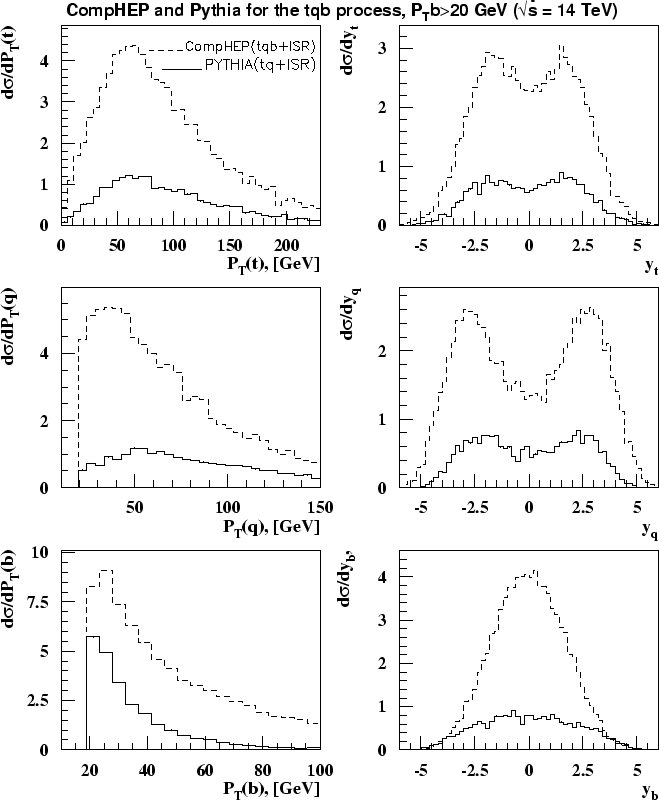
обрезания ![]() ГэВ вычисленное полное сечение
(116 pb) в несколько
раз выше, чем сечение полученное в PYTHIA (25.4 pb). Соответствующие распределения показаны
на рисунке 1.5, из которых ясно видно, что приближение функции
расщепления в PYTHIA дает существенно меньший вклад в жесткой области
и, как можно было ожидать, не описывает полные вычисления. С другой стороны,
древесные вычисления не учитывают существенные КХД коррекции для мягкого
ГэВ вычисленное полное сечение
(116 pb) в несколько
раз выше, чем сечение полученное в PYTHIA (25.4 pb). Соответствующие распределения показаны
на рисунке 1.5, из которых ясно видно, что приближение функции
расщепления в PYTHIA дает существенно меньший вклад в жесткой области
и, как можно было ожидать, не описывает полные вычисления. С другой стороны,
древесные вычисления не учитывают существенные КХД коррекции для мягкого
![]() кварка, которые можно учесть включением процесса с
кварка, которые можно учесть включением процесса с ![]() в начальном состоянии,
что сделано в PYTHIA. Следовательно, что бы корректно воспроизвести кинематические
свойства во всем фазовом пространстве и не допустить двойного счета, надо
правильно объединить оба способа вычислений.
в начальном состоянии,
что сделано в PYTHIA. Следовательно, что бы корректно воспроизвести кинематические
свойства во всем фазовом пространстве и не допустить двойного счета, надо
правильно объединить оба способа вычислений.
Основной вклад NLO поправок приходится на ``мягкую'' кинематическую область.
Как было указано выше, полные NLO вычисления для ![]() -канального процесса
дают полное сечение равное 245 pb. Для включения известных NLO результатов была использована
следующая нормализация для ``мягкой'' области:
-канального процесса
дают полное сечение равное 245 pb. Для включения известных NLO результатов была использована
следующая нормализация для ``мягкой'' области:
В результате, берутся события для ``жесткой'' кинематической
области с
![]() , приготовленные генератором SingleTop, и события,
приготовленные для ``мягкой'' области в PYTHIA с
, приготовленные генератором SingleTop, и события,
приготовленные для ``мягкой'' области в PYTHIA с
![]() .
Остается найти такое значение
.
Остается найти такое значение
![]() , что бы комбинированные
, что бы комбинированные ![]() распределения
были гладкими. На рисунке 1.6 показаны распределения для значения
распределения
были гладкими. На рисунке 1.6 показаны распределения для значения
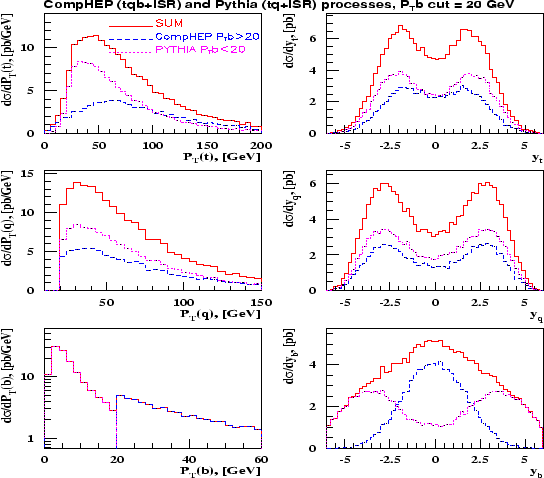
![]() ГэВ. Можно видеть большой уступ в распределении по
ГэВ. Можно видеть большой уступ в распределении по ![]() .
После несложного анализа было найдено, что значение
.
После несложного анализа было найдено, что значение
![]() ГэВ
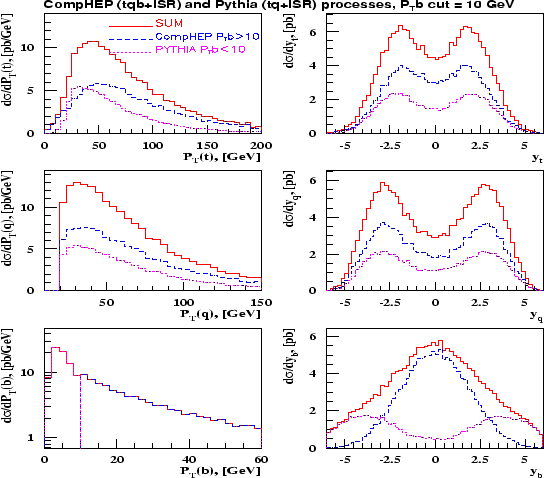
удовлетворяет нужным требованиям. Соответствующие распределения показаны на
рисунке 1.7. Комбинированное распределение по
ГэВ
удовлетворяет нужным требованиям. Соответствующие распределения показаны на
рисунке 1.7. Комбинированное распределение по ![]() достаточно гладкое
и, следовательно, корректное объединение ``мягкой'' и ``жесткой'' области найдено.
достаточно гладкое
и, следовательно, корректное объединение ``мягкой'' и ``жесткой'' области найдено.
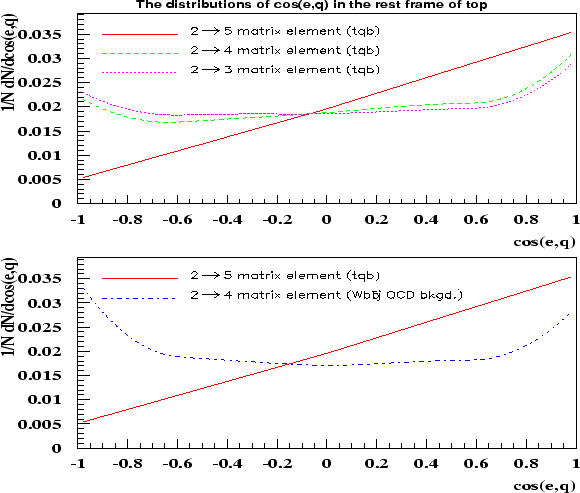 |
С целью правильного учета всех спиновых корреляций рождения топ-кварка и его распада
в генератор SingleTop были включены полные матричные элементы, включающие все распады.
Соответственно для процесса ![]() матричный элемент включает в себя следующий процесс:
матричный элемент включает в себя следующий процесс:
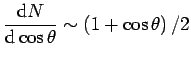 |
(1.11) |
С помощью описанного генератора SingleTop была создана база данных событий, связанных с рождением одиночного топ-кварка; для коллаборации CMS (LHC) проводится моделирование отклика детектора и планируется использование смоделированных событий в физическом анализе данных.